On BatchedNMS Implementation in Torchvision
Recently I was going through torchvision’s batched nms implementation. Batched NMS lives
in torchvision/ops/boxes.py in a function named batched_nms.
These lines caught my attention:
if boxes.numel() > (4000 if boxes.device.type == "cpu" else 20000) and not torchvision._is_tracing():
return _batched_nms_vanilla(boxes, scores, idxs, iou_threshold)
else:
return _batched_nms_coordinate_trick(boxes, scores, idxs, iou_threshold)
When you perform batched nms, torchvision actually chooses between two implementations based on number of input boxes. For larger inputs, it calls
_batched_nms_vanilla which is defined in the same file. This function
works as you would expect, it separates boxes by class id and then performs nms for each group. _batched_nms_coordinate_trick is more interesting as
it uses a smart trick to do multi-class nms in a single nms pass.
Let’s suppose you run an object detector and got several bounding boxes for each class (3 in this example). Now you need to perform NMS to get rid of duplicate overlapping boxes. Normally, you would do NMS for each class separately. That is if there are 2 overlapping boxes belonging to different classes, neither should be eliminated as they designated different objects.
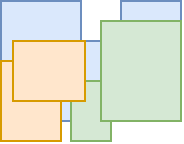
What _batched_nms_coordinate_trick does is it adds offsets to bounding boxes of the same class which gurantees zero overlap between boxes of different classes.
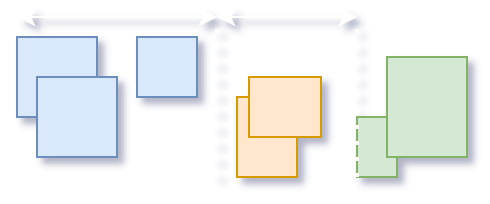
Then, these offsets are subtracted from the resulting coordinates and we get the same result.
There is actually a whole thread on this issue. I decided to run my own benchmark and got this result for 80 classes (averaged over 3 trials):
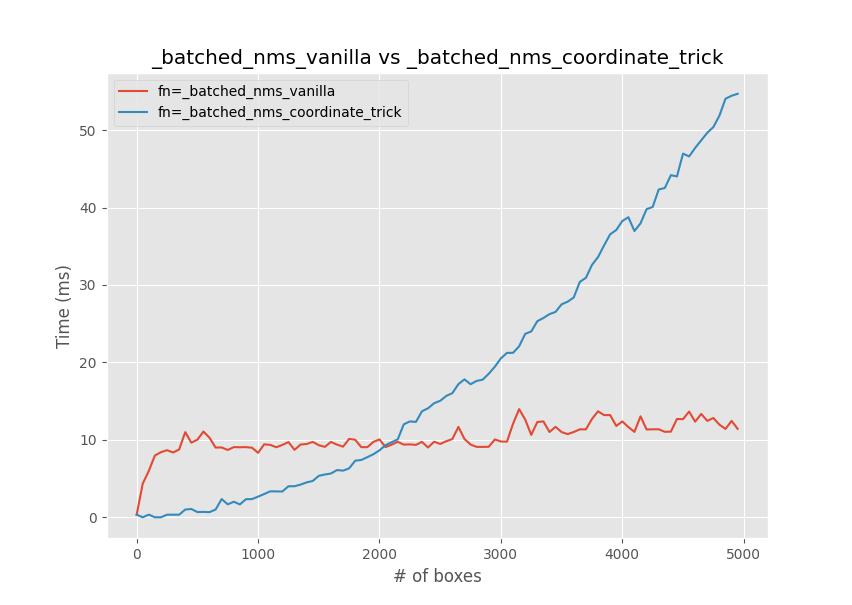
_batched_nms_coordinate_trick is actually faster for smaller inputs (though on my PC the threshold seems to be around 2000 boxes rather than 1000).
This is an interesting way to do batched nms, however it seems counter-intuitive. Torchvision implements NMS in \( O(n^2) \) time. Math tells us that for \( O(n^2) \) algorithm an increase in input size by a factor \( t \) will result in \( (tn)^2 = t^2(n^2) \) increase in runtime. On the other hand, running the algorithm \( t\) times separately gives us \( t(n^2) \) which means linear complexity with respect to the number of classes.
My best guess here is that _batched_nms_vanilla has an overhead due to tensor masking and conditionals which are relatively expensive operations, though this requires a more in-depth profiling of PyTorch’s code
which I might do in the future.