Realistic kite flight
The other day I was going through my old projects archive. I stumbled upon this indie puzzle game that I abandoned a long time ago, as it was taking too much time.
The game itself is not technically challenging in any way, however there’s one part I really liked working on. During the entire game, the player is supposed to chase a flying paper kite. The kite was the single most important element, so it had to fly gracefully and smoothly.
To begin with, I made a low-poly kite model in Blender and slapped a picture of Japanese waves on it, which automatically made it 10 times better.
Then, I imported the model into Unity and used cloth simulation component to make the tail wiggle when moved.
Now, the kite was supposed to fly through predefined points in the world. In the beginning, the kite’s position can be set to the first point. However, there are many ways to move to the next point. As expected, linear interpolation between points produced unrealistic trajectories which are not worth exploring.
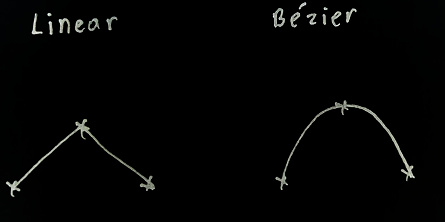
To get a nice smooth and curvy path, I decided to use Bezier curves as they are easy to work with and there is a convenient plugin for Unity.
Great! Now we have a flight trajectory that is better than linear interpolation! Our next problem is deciding how to move along this curve. Path Creator plugin provides us with two convenient functions - GetPointAtDistance() and GetRotationAtDistance(). They both accept a distance parameter which you can think of as the offset along the curve (\( t \) in the plot below). They return coordinates and orientation of a point at the specified offset.
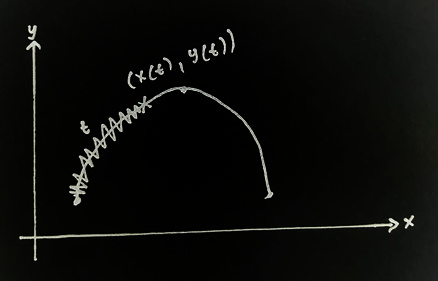
We can increase this offset at a constant speed and use these functions to get the point of the trajectory to put our kite at. However, we know that things that rise slow down and things that fall accelerate, so we can’t simply use constant speed.
Let’s say our kite starts at point \( K_0 \) with initial altitude \( y_0 \) and speed \( v_0 \) and moves to point \( K_n \) with altitude \( y_n \) and speed \( v_n \).
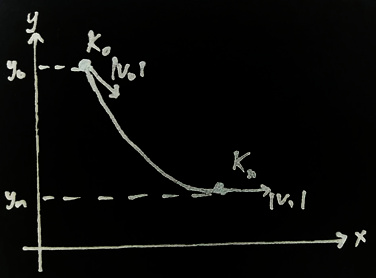
Energy conservation law says that the total energy of the system doesn’t change, so:
\[ \Delta E_k = -\Delta E_p \]
We define \( E_k = \frac{1}{2}mv^2 \) and \( E_p = mgy \), then:
\[ g \left( y_n - y_0 \right) = -\frac{1}{2} \left( v_n^2 - v_0^2 \right) \]
As \( y \) must be a point on the curve, we solve the equation for \( v_n \), which gives us:
\[ v_n(y_n) = \pm \sqrt{v_0^2 - 2g \left( y_n - y_0 \right)} \]
This equation gives us a realistic magnitude of speed at any altitude \( y_n \) which is given by the Bezier curve. Now we can keep track of the traveled distance and adjust the speed using the final formula. Let’s put it all together in a Unity component:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using PathCreation;
public class Kite : MonoBehaviour {
public PathCreator path;
public float initialSpeed = 10;
public float g = 9.8f;
public EndOfPathInstruction end;
private float dstTravelled;
private float speed;
private float yInit;
void Start() {
yInit = transform.position.y;
speed = initialSpeed;
}
void Update() {
dstTravelled += speed * Time.deltaTime;
float dh = transform.position.y - yInit;
speed = Mathf.Sqrt(Mathf.Max(initialSpeed * initialSpeed - 2 * g * dh, 0));
transform.position = path.path.GetPointAtDistance(dstTravelled, end);
transform.rotation = path.path.GetRotationAtDistance(dstTravelled, end);
}
}
In cases when the target point is too high and there’s not enough energy to reach it, we get a negative number under the square root (\( v_0^2 - 2g \left( y_n - y_0 \right) < 0 \)). Here I clamp the value at 0 to avoid runtime errors, but the kite would be stuck at one point because the speed is 0. In the real world, kite might get additional energy from the wind, but that’s beyond the scope of what I was doing.
Below you can see the final result of combining Bezier curves and energy conservation.
The key here is to use as few points as possible to avoid unrealistic sharp turns and balance initial height with initial speed. There are probably many other ways to make it look even better, which I might implement in the future.